5.4 Atividade #3

Essas duas equações de primeira ordem acopladas

$\displaystyle \frac{dy}{dt} = p; \frac{dp}{dt} = -4\pi ^2 y$

(5.4.1)

Lembrando que: $\displaystyle \frac{d^2 y}{dt^2} = \frac{d}{dt} \left( \frac{dy}{dt} \right ) = \frac{dp}{dt} = -4\pi ^2 y$

define um movimento harmônico simples de período 1. Pela generalização de uma das variáveis das fórmulas acima para esse caso de duas variáveis, integre essas equações com qualquer condição particular inicial de sua escolha (desde que faça sentido, obviamente) e verifique com qual acurácia o sistema retorna para o seu estado inicial para os valores de $t$ . Utilize os modos de Euler e Runge-Kutta e compare os métodos.

Dica

Pelo método de Euler temos:

$\displaystyle f(t,p)=-4\pi ^2y \Longrightarrow p_{n+1}=p_n + \Delta t\ f(t,p)$

(5.4.2)

encontrando os valores de $p$ podemos calcular os valores de $y$

$\displaystyle f(t,y)=p \Longrightarrow y_{n+1} = y_n + \Delta t\ f(t,y)$

(5.4.3)

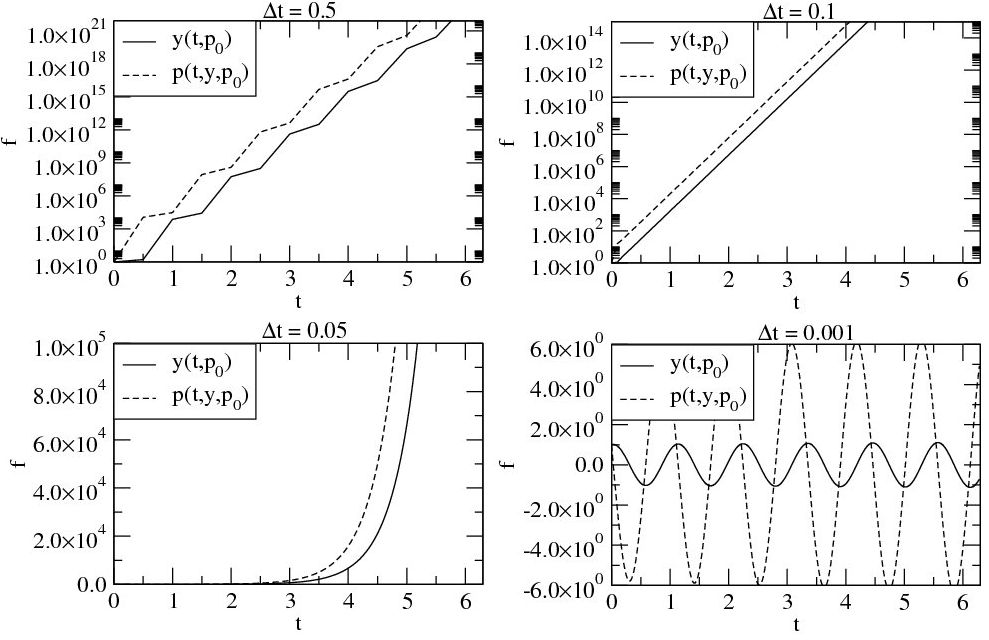
Agora, utilizando esta idéia, implemente o mesmo sistema com o algoritmo de Runge-Kutta. Deveremos obter gráficos semelhantes aos gráficos das figuras 5.1, 5.2 e 5.3.

Parte do código para o cálculo da eq. 5.4 pelo método de Euler. Lembrando que aqui utilizo vetores. Não é necessário utilizar vetores!!!

! EULER
do i = 1, n-1
  t(i+1) = t(i) + dt1
  p(i+1) = p(i) + dt1 * ( -4.d0 * pi**2 * y(i) )
  y(i+1) = y(i) + dt1 * p(i)
end do

Parte do código para o cálculo da eq. 5.4.1 pelo método de Runge-Kutta de quarta ordem. Lembrando que aqui está utilizo vetores. Não é necessário utilizar vetores!!!

! RUNGE-KUTTA 4 ORDEM
do i = 1, n-1
  ! CALCULANDO PONTOS Pn
  ! TERMOS DO RK4
  kp1 = dt1 * ( -4.d0 * pi * pi * rk4y(i) )
  kp2 = dt1 * ( -4.d0 * pi * pi * ( rk4y(i) + 0.5d0 * kp1 ) )
  kp3 = dt1 * ( -4.d0 * pi * pi * ( rk4y(i) + 0.5d0 * kp2 ) )
  kp3 = dt1 * ( -4.d0 * pi * pi * ( rk4y(i) + kp3 ) )
  ! y(n+1) = y(n) + 1.0/6.0 (k1+2*k2+2*k3+k4)
  ! r6 = 1.d0/6.d0
  rk4p(i+1) = rk4p(i) + r6 * (kp1 + 2.d0*kp2 + 2.d0*kp3 + kp4)

  ! CALCULANDO PONTOS Yn
  ky1 = dt1 * ( rk4p(i) )
  ky2 = dt1 * ( rk4p(i) + 0.5d0 * ky1 )
  ky3 = dt1 * ( rk4p(i) + 0.5d0 * ky2 )
  ky4 = dt1 * ( rk4p(i) + ky3 )
  ! y(n+1) = y(n) + 1.0/6.0 (k1+2*k2+2*k3+k4)
  ! r6 = 1.d0/6.d0
  rk4y(i+1) = rk4y(i) + r6 * (ky1 + 2.d0*ky2 + 2.d0ky3 + ky4)
end do

**Figura 5.1:** Integração das equações 5.4.2 e 5.4.3 para intervalos de tempo iguais a , , e

**Figura 5.2:** Integração da equação 5.4.1 utilizando o método de Runge-Kutta para intervalos de tempo iguais a , , e .

**Figura 5.3:** Integração utilizando os métodos Euler e Runge-Kutta para o $\Delta t = 1.0 \times 10^{-5}$ .